DFS

DFS介绍

DFS，即深度优先搜索，经常用于暴力以及图上遍历等。相比于bfs,dfs是纵向的搜索，是一次性找到底的。从根找到底，然后退回来换条路继续走到底，直到走完。

DFS可以理解为是递归+回溯。对于一棵DFS树，其搜索的方式是从根结点开始，沿着一条边一直走到底，层层递归，每次进入一个子节点就可以理解为一个新的以此子节点为根的DFS树，称之为递归。当访问到叶子结点时，又需要将叶子结点的信息返回并总结到该叶子节点的父亲节点，称之为回溯。

DFS大部分分为树上DFS与图上DFS，但其实两者是相通的，图上DFS可以将上下左右四个方向的遍历结果转化为该位置的四个儿子结点，此时还需要一个vis数组用来记录该儿子结点是否在别的分支出现过，尽管从一个点到另一个点会有多条路径，但如果不是要求最短路径的情况下，往往只需要记录一次即可。

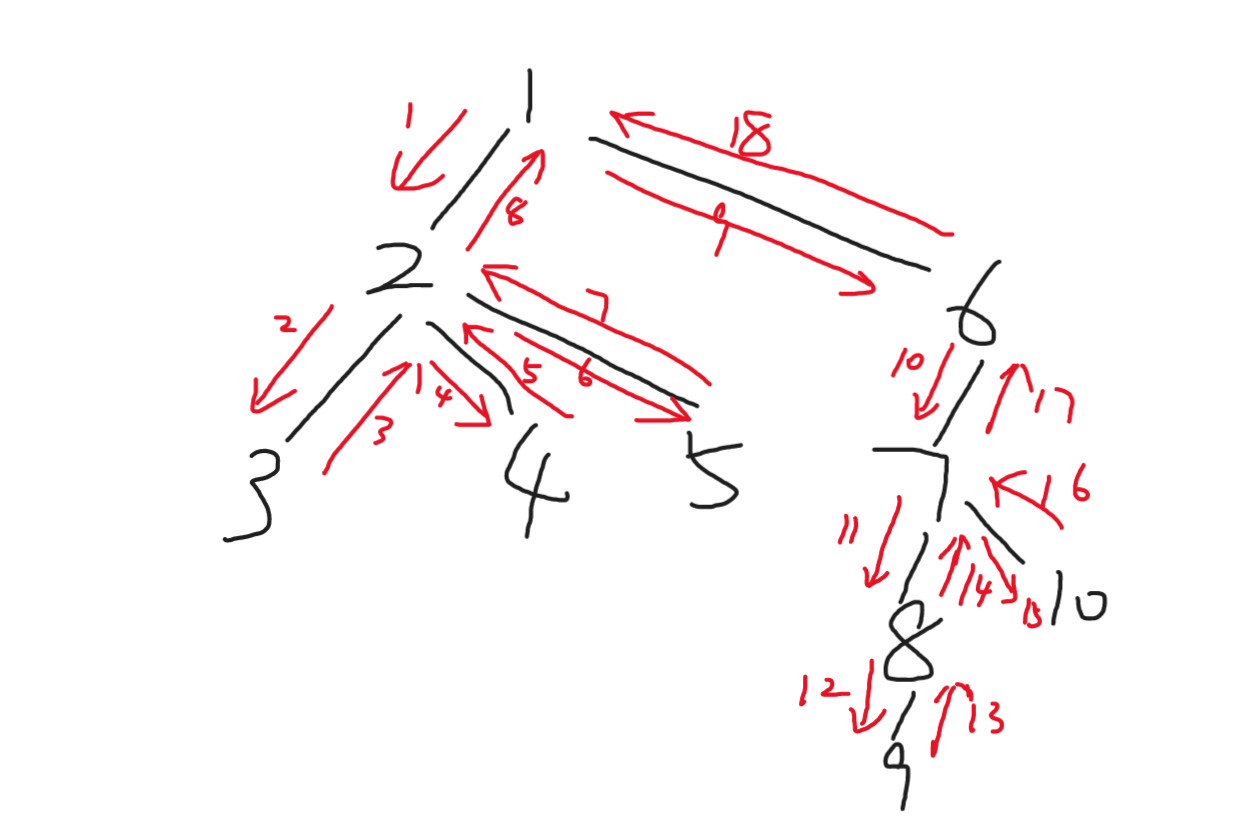
DFS模板

int dfs(int u){//树上dfs,该样例用于求这棵树的权值和
    int sum=w[u];
    for(int i=0;i<cnt[u];i++){//cnt[u]表示u的子节点个数
        sum+=dfs(son[u][i]);//遍历u的第i个儿子
    }
    return sum;
}


int d[4][2]={{1,0},{-1,0},{0,1},{0,-1}};//四个方向上x,y轴分别的变化量
void dfs(int x,int y){//x,y表示当前位置坐标，tx,ty表示目标位置坐标，该样例表示遍历图上每一个点
    if(vis[x][y])return;//如果该点访问过就不访问了
    vis[x][y]=1;
    for(int i=0;i<4;++i){
        int dx=x+d[i][0],dy=y+d[i][1];//原先的x轴方向的值再加上变化量就是现在的x值
        if(dx<0||dx>=n||dy<0||dy>=m)continue;//超出边界就不过去了
        dfs(dx,dy);
    }
}

写在末尾

以上都是比较明显的dfs搜索，但是很多时候遇到的情况都需要将题意向dfs树的转化，例如全排列，那么每一个结点的子节点就是所要排列的所有数，如果要求数字不重复只需添加vis数组记录即可，但是每次回溯后需要对该vis值清空。同样，作为常见的暴力拿部分分的神器，我们也可以依靠dfs枚举每一步或者每一个物品的状态，这样虽然时间复杂度到了阶乘或指数级别，但是足以拿一些部分分了。