lambda表达式的理解

lambda表达式的具体定义可以去网上找，我对它的理解就是将一个函数以更简洁的方式，以表达式的形式内嵌在某个函数中。

lambda表达式的应用场景

lambda表达式最常用的是在sort函数中，把cmp函数以lambda表达式直接写在内部，代码如下:

1
2
3

sort(a.begin(),a.end(),[&](int x,int y){//此排序采用降序排序
   return x>y; 
});

等价于

1
2
3
4

bool cmp(int x,int y){
    return x>y;
}
sort(a.begin(),a.end(),cmp);

题意

给定一串字符串，求其中有多少长度>=3子串，且该子串中某个字符只出现一次。

思路

最终答案的求取可以通过遍历以i位置为所要求的只出现一次的字符所对应的子串数量来求取。

然后显然我们不可能直接对于每个字符c，都暴力的去找左边有多少个相邻的连续的连续的字符与c不同，以及右边有多少个相邻的连续的连续的字符与c不同。于是，我们需要通过预处理，来记录每个字符左右两边分别有多少个相邻的、连续的、与此字符不同的字符，最终的答案也可以理解为左边挑，右边取，然后相乘即可。假设左边的个数为l，右边的个数为r。那么对于该字符，它的贡献为:

由于还有一个限制是长度>=3，所以对某一边没有符合要求的字符时，需要另一边减去只取一个字符的情况，即：

BFS

BFS介绍

BFS，即宽度优先搜索，经常用于图上遍历等。相比于dfs,bfs是横向的搜索，是一层一层找的。

BFS通过队列进行依次处理，对于每个结点的子节点，将它通过排队的形式排在这一层的后面而非直接遍历，对于一颗BFS树，它的BFS序便是一层一层的向下拓展。

同时BFS由于是层层遍历，先访问到的一定是距离初始点最短的。

DFS

DFS介绍

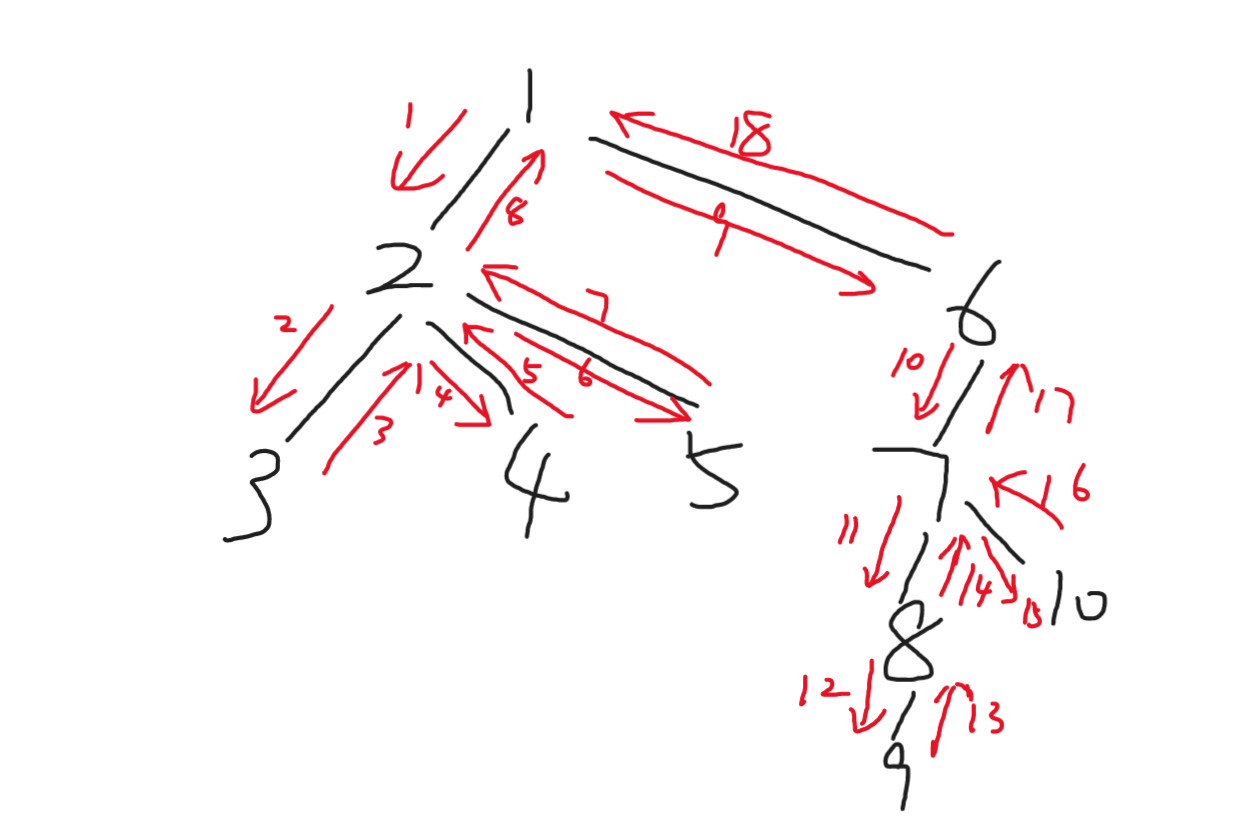
DFS，即深度优先搜索，经常用于暴力以及图上遍历等。相比于bfs,dfs是纵向的搜索，是一次性找到底的。从根找到底，然后退回来换条路继续走到底，直到走完。

DFS可以理解为是递归+回溯。对于一棵DFS树，其搜索的方式是从根结点开始，沿着一条边一直走到底，层层递归，每次进入一个子节点就可以理解为一个新的以此子节点为根的DFS树，称之为递归。当访问到叶子结点时，又需要将叶子结点的信息返回并总结到该叶子节点的父亲节点，称之为回溯。

DFS大部分分为树上DFS与图上DFS，但其实两者是相通的，图上DFS可以将上下左右四个方向的遍历结果转化为该位置的四个儿子结点，此时还需要一个vis数组用来记录该儿子结点是否在别的分支出现过，尽管从一个点到另一个点会有多条路径，但如果不是要求最短路径的情况下，往往只需要记录一次即可。

题意

给定一张二维图，图上有两个连通块，求使得两个连通块相连的最短路径。

思路

由于无法区分两个连通块，所以通过dfs对两个连通块中的元素分别赋值0/1，然后对于两个连通块中的所有点分别求曼哈顿距离-1即可。（曼哈顿距离：水平距离+竖直距离）

前言

由于前缀和和差分一个加一个减，两个在写法上差距不大而且具有一定共同点，所以放在一块进行描述。

前缀和

前缀和介绍

前缀和顾名思义，就是一段数列前面某一段连续数列的和。

他经常用于预处理区间和的信息，通过预处理前缀和，我们可以快速的得到某段连续数列的和是多少。

当我们需要求取的区间和时，我们可以用来获取，经常会有人将减号后面写成，但是我们需要保留的和，需要减去的重复部分应该是之前的部分

题意

给定，求与范围内与互质的数的个数

思路

​ 这个就是欧拉函数的定义。

首先根据唯一分解定理可得：设，其中为质数，有

，其中后面连乘的部分与 无关，那么可以直接由来获取所有，直接分解质因数即可。对于，根据同余，可以通过快速幂得到。答案要求对大质数取余，除某个数等于乘该数的余数减二次方，即就是逆元。

题意

给定n位字符串，可以对连续的几位都进进行+1/-1的操作，求变成目标串最少的操作次数

思路

这里涉及到一个概念叫做相对距离，对于从起始串到目标串的变化可以转化为0000串到某个串的变化，每一位的相对距离保持不变即可。

这样我们就只需要预处理求出0000串到所有状态的最小操作次数即可，可以通过BFS来求出并记录。

题意

给定长度为n的数列，求出连续序列和为k的倍数的序列个数。

思路

首先，对于每一段前缀和都进行对k取余。

那么根据同余定理，,如果一段前缀和如果和前面的某段前缀和的值相同，那么前面的那个前缀所缺少的几个数（除最后一个元素）的和一定是k的倍数，对于每个余数所对应的前缀和数量，用一个map记录一下即可。

最后记得再加上，因为每次前缀和所得的那几个数并不包括尾部，所以当遍历到最后一个元素时，并无法得出包括最后一个元素的符合条件的连续序列数量，而是包括最后一个前面的那个元素的符合条件的连续序列数量。

题意

几间房间有各自的温度，每次操作可以对连续的几间房间+1/-1度，请问使每个房间都到达目标温度的最小操作次数

思路

​ 将目标温度减去起始温度后会得到一串数列a，目标就是求使这串数列全部为0的操作次数，由于需要实现区间加，比较容易联想到使用差分来进行操作。

​ 转化为差分数组后，每次操作就可以转化为对于某个位置+1/-1，在对某个位置-1/+1，或者不存在后者（就是位置为数列尾部+1）。

​ 这样就只需要比较到底是+1的次数多还是-1的次数多即可